PCA and SVD for Big Data Matrices
Our Matlab implementation of randomized principal component analysis is available here.
Huamin Li, George C. Linderman, Arthur Szlam, Kelly P. Stanton, Yuval Kluger, and Mark Tygert. 2017. Algorithm 971: An Implementation of a Randomized Algorithm for Principal Component Analysis. ACM Trans. Math. Softw. 43, 3, Article 28 (January 2017), 14 pages. DOI: https://doi.org/10.1145/3004053
|
Fig. 1 Comparison of our Matlab routines for principal component analysis with the built-in Matlab routines “svd” and “svds”. The figures graph the running-times of the routines “svd,” “svds,” and “pca” (“pca” is our implementation of the randomized algorithm) for matrices with equal number of rows and columns (m=n). For each routine we show left, middle and right bars that correspond to matrix sizes of m=n=1000,10000 and 100000 respectively. Smaller bars in the graph correspond to better performance. The figures on the left and right panels correspond to rank k=10 and k=100 approximations respectively. The accuracy of our algorithm is always superior to Matlab's "svds" and never more than half a digit worse than the 5-digit accuracy of the low-rank approximation produced by Matlab's "svd". Neither routine “svd” nor routine “svds” was able to process the matrix of size 100,000 x 100,000; “svd” would take an inordinate amount of time, while “svds” ran out of memory. |
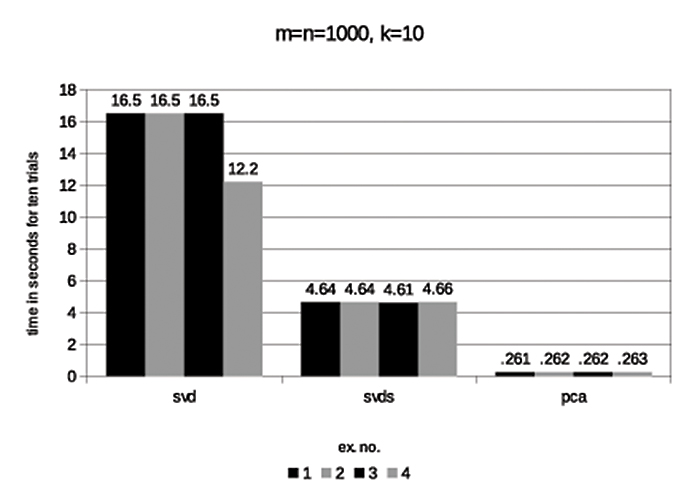
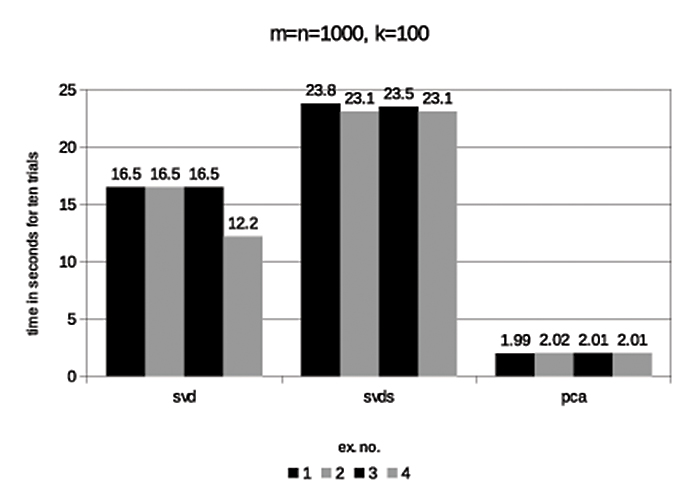
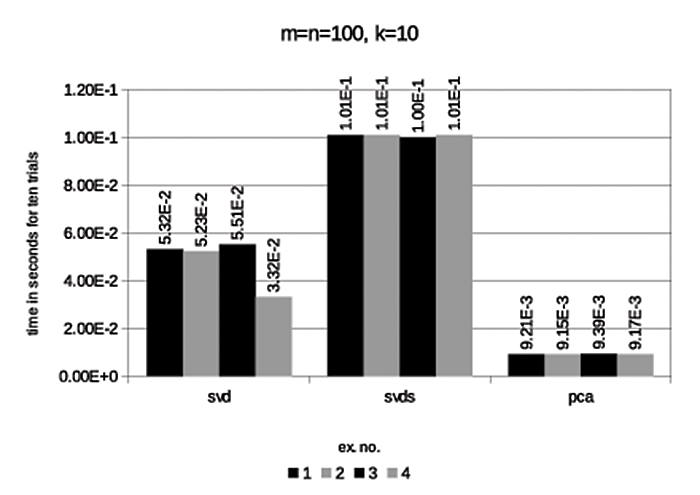
Fig. 2
Running-times for 10 trials of the routines “svd,” “svds,” and “pca” (“pca” is our implementation of the randomized algorithm). The four examples concern four classes of matrices, each with a different distribution of singular values (such that the best possible rank-k approximation USV* satisfies ||A-USV*|| = 10-5). The accuracy of our algorithm is always superior to Matlab's "svds" and never more than half a digit worse than the 5-digit accuracy of the low-rank approximation produced by Matlab's "svd".